川渡り問題の一般化を考える

投稿:2025/11/17 更新:2025/12/01

はじめに

川渡り問題とはなにか

舟を使い特定の条件を満たしながらすべての対象を対岸へ運ぶ論理パズル。
いくつかバリエーションがあるが、有名な例を一つ挙げる

狼とヤギとキャベツ

オオカミとヤギを連れ、キャベツを持った農夫が川岸にいる。川には1艘の舟がある。
舟を漕げるのは農夫のみ。
舟には農夫のほか、動物1頭かキャベツ1個しか乗せられない。
農夫がいないときに
- オオカミとヤギを岸に残すと、オオカミがヤギを食べてしまう。
- ヤギとキャベツを岸に残すと、ヤギがキャベツを食べてしまう。

すべてを無事に対岸に渡すにはどうしたらよいか?
wiki参照

解答例

オリジナルの川渡り問題

草, バッタ, カエル, イタチ, タカ, を連れた農夫が川岸にいる。川には1艘の舟がある。

舟を漕げるのは農夫のみ

舟には農夫の他、2つの対象を乗せられる。

農夫がいないときに、

タカとイタチを残すと、タカがイタチを食べてしまう

イタチとカエルを残すと、イタチがカエルを食べてしまう

カエルとバッタを残すと、カエルがバッタを食べてしまう

バッタと草を残すと、バッタが草を食べてしまう

イタチと草を残すと、イタチが草を食べてしまう

すべてを無事に対岸に渡すにはどうしたらよいか

オリジナル問題といっても、大まかな設定は「狼とヤギとキャベツ」とほぼ同じ

川渡り問題の一般化

原題とオリジナル問題の違いは、「対象の集合」「食う食われる関係」「舟の容量」のみ。
これらを抽象化して一般化した川渡り問題を定義する。

運ぶ対象の集合
$X$
食う食われる関係の集合
$F \subseteq X \times X$
舟のサイズ(農夫以外で一度に乗れる最大数)
$B$

ルールを「グラフ」で表現する

対象集合$X$ を頂点集合、食う食われる関係 $F$ を辺として見ることでグラフを作る。
AがBを食べるという関係は一見有向辺のように思えるが、今回は違反が発生するかどうかのみが重要なので無向辺でよい。

具体例

狼とヤギとキャベツ
ボートサイズは1

  graph LR
    オオカミ <--> ヤギ
    ヤギ <--> キャベツ

単純なパスになる。

オリジナル問題
ボートサイズは2

  graph LR
    タカ <--> イタチ
    イタチ <--> カエル
    カエル <--> バッタ
    バッタ <--> 草
    イタチ <--> 草

グラフとして見ると禁止ペアの関係を視覚的に理解しやすい。

最小ボートサイズの考察

一般化川渡り問題は、ボートサイズ$B$とグラフ$G(X,F)$によって表現できることがわかった。
では、$B$と$G$が与えられた時、川渡りが可能かどうかを判定する問題を考えてみよう。
グラフ$G$に対して$Boat(G)$を、川渡りを成功させるために必要な最小のボートのサイズと定義したとき、この問題の答えは$B \geq Boat(G)$ならば可能、$B < Boat(G)$ならば不可能である。
$Boat(G)$はどのような値になるだろうか。
$Boat(G)$を厳密に求めるのは難しいが、大まかに絞り込んでみる。

下界を考える

初手で左岸に残しておく頂点集合の間に1つでも辺が貼られてあってはいけない(独立集合 - Wikipedia)。
逆に言えば、初手で船に乗せる頂点集合は頂点被覆 - Wikipediaを成していないければならない。
グラフGの最小頂点被覆のサイズを$\tau(G)$と置くと、初手で最低でも$\tau(G)$頂点をボートに乗せる必要がある。
したがって$\tau(G)\le Boat(G)$という下界が得られる。

上界を考える

では$Boat(G)$が常に下界の$\tau(G)$に一致すると言えるだろうか。
以下のような例を考えてみる。

  graph LR
    0 <--> 1
    0 <--> 2
    0 <--> 3

このグラフの最小頂点被覆は${0}$で、$\tau(G)=1$である。
実際に試してみたい人はこちらのサイトのFに以下を貼り付けて実験してみてほしい
River Crossing

答えを言うと、このグラフは$Boat(G)=2$であり、サイズ1のボートでは達成不可能。

無駄な往復(集合aを運び、直後にaを戻す)を行わないようにし、グラフの対称性を利用すると
0を右岸に運ぶ
左岸に移動
1を右岸に運ぶ
0を左岸に運ぶ

の一本道しかなく、次に有効な操作は存在しないので詰み。

もし、ボートサイズが2なら、頂点0を常に船に載せながら、頂点1,2,3を一つずつ運んでいくことで達成できる。
そしてこれは一般のグラフでも使える戦略で、ボートサイズが$\tau(G)+1$ならば、最小頂点被覆の頂点を常に舟に乗せながら、一つの空きを使ってそれ以外の頂点(最大独立集合)を一つずつ運んでいくことで、必ず川渡りを達成させることができる。

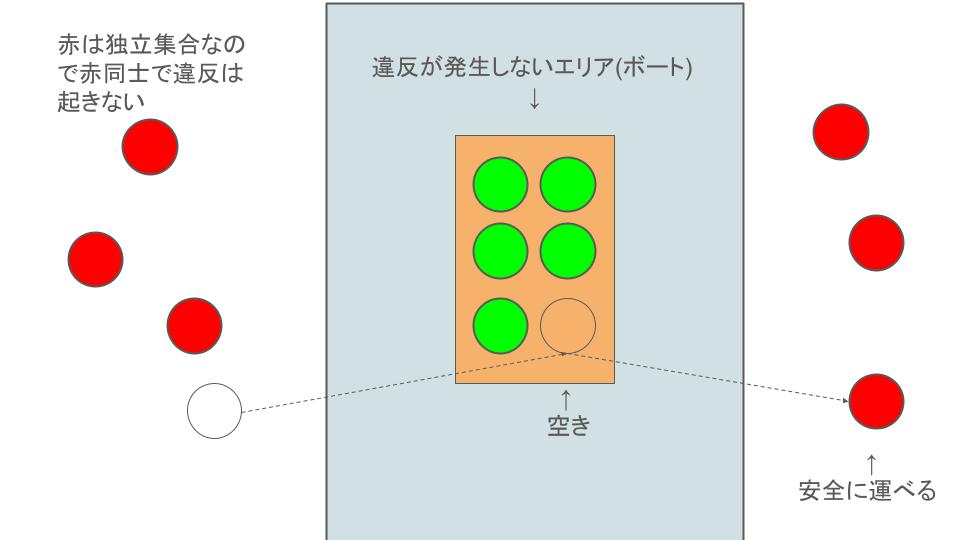
したがって$Boat(G)\le \tau(G)+1$という上界が得られる。

以上より

$$ Boat(G) = \begin{cases} \tau(G) \\ \tau(G)+1 \end{cases} $$ が成り立つ。最小頂点被覆(および最大独立集合)のサイズさえ分かれば、最小ボートサイズ$Boat(G)$は二択に絞り込むことができる。
この2択を特定するのは難しいので次の記事に回すが、一般化川渡り問題をグラフとして解釈することで、グラフの最小頂点被覆と最小ボートサイズに深い関係があることがわかった。

アルクイン数

「狼とヤギとキャベツのルール」をグラフとして解釈する発想は自然なようで、2000~2010年代に研究された記録が残っている。
グラフGに対する最小ボートサイズ$Boat(G)$はグラフのアルクイン数(Alcuin Number) と呼ばれている。
アルクイン数を高速に計算する問題は一般的には非常に難しい問題(NP困難)であることが証明されているが、特定のグラフクラス(木とか)では効率的に解ける場合がある。

詳しくは以下の論文に記されている。
Seify, A., & Shahmohamad, H. (2014). Some New Results in the Alcuin Number of Graphs. arXiv preprint arXiv:1409.6949. https://doi.org/10.48550/arXiv.1409.6949

(ちなみに、階層的なグラフ(生態系ピラミッド状？・多層パーセプトロン状？)なら多項式時間で計算することができる)
論文に記されている定理や、詳しいアルゴリズムは次の記事で紹介したい。
川渡り問題の一般化を考える ② アルクイン数と実装

ブラウザゲーム

River Crossing
ステージ1が狼とヤギとキャベツ
ステージ2~7がオリジナル問題で、3はこの記事で紹介した問題。5以降は適当